The Magic Hexagon
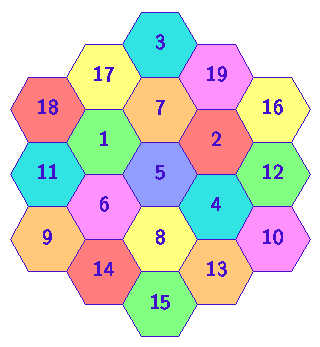
By the "diameter" of a potential magic hexagon, I mean the number of hexagonal cells in the longest row. The diameter must be an odd integer.
The diameter-1 hexagon has one cell, the diameter-3 hexagon has 2+3+2 = 7 cells, the diameter-5 hexagon (pictured above) has 3 + 4 + 5 + 4 + 3 = 19 cells, etc. In general, the hexagon of diameter 2k-1 has
| C(k) | = | k + (k+1) + (k+2) + ... + (2k-2) + (2k-1) + (2k-2) + (2k-3) + ... + k |
| = | 3k(k-1) + 1 |
cells.
We wish place the integers from 1 to C(k) into the cells of the hexagon of diameter 2k-1. The sum of the values in all cells is given by S(k)=C(k)(C(k)+1)/2. Considering, say, the vertically oriented rows (of which there are 2k-1), the average row sum is R(k)=S(k)/(2k-1). For example, in the diameter-5 hexagon, we have k=3, and R(3) = 38, which is the common row sum in the magic hexagon pictured above.
In general, for a hexagon of diameter 2k-1 to have the property that all row sums are equal, it is necessary for R(k) to be an integer. However, since
| R(k) | = | (3k2 - 3k + 1) (3k2 - 3k + 2) / (4k - 2) |
| = | (1/32)(72k3 - 108k2 + 90k - 27 + 5/(2k-1)), |
we see that in order for R(k) to be an integer, it is necessary for 5/(2k-1) to be an integer, which (for positive values of k) occurs only if k is either 1 or 3. Thus 1 and 5 are the only possible magic hexagon diameters.
Frank R. Kschischang, Sept 23, 2000.